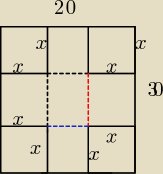
optymalizacja Saizou : z prostokątnej kartki o wymiarach 20x30 cm wycięto kwadraty. Z pozostałej części zbudowano pudełko. Oblicz wymiary wyciętych kwadratów tak aby pole powierzchni podstawy pudełka było najmniejsze. niebieski odcinek ma długość 20−2x czerwony odcinek ma długość 30−2x P_podstawy=(20−2x)(30−2x)=600−50x+4x²=4x²−50x+600 f(x)=4x²−50x+600

	−b		50
fmin=p=		=		=6,25cm
	2a		8

zatem wymiar jednego kwadratu musi być równy 6,25x6,25 mógłby ktoś to sprawdzić?

Saizou : oj poprawka f(x)=4x²−100x+600 p=12,5 zatem wymiary 12,5x12,5

Saizou : up.

Saizou :

Saizou : ale coś mi nie pasuje bo z założeń wyjdzie że x<10

Basiek: Błażej− skąd to zadanie? Bo błędu u Ciebie nie ma.

Saizou : z sprawdzianu z matematyki i po prostu nie wiem

Basiek: Moim zdaniem, należy znaleźć maksimum lokalne

Saizou : proszę mówić mi po polskiemu

Basiek: Średnio wiem, co to jest, nie umiem tego policzyć; ale zdecydowanie mądrze brzmi.

Basiek: http://pl.wikipedia.org/wiki/Ekstremum

Saizou : zdecydowanie mądrze a raczej za mądrze

Basiek: Wiem. Ale błędu naprawdę nie ma. [nie widzę]

Saizou : ja też nie tylko że wymiar 12,5x12,5 jest nie realny

Basiek: Owszem, masz warunek x∊(0,10)

Basiek: Ale na pewno pole podstawy pudełka?

psik: a może nie pole podstawy a pole całego pudełka? Jesteś pewny co do treści zadania?

Saizou : tak pole podstawy ma być jak najmniejsze

psik: , widzę że myślimy podobnie

Basiek: To dobrze o mnie świadczy. To nie ma innej opcji niż znaleźć ekstremum lokalne. Po prostu. Tego zwykłym "wierzchołkiem" nie policzysz.

Saizou : na pewno było pole podstawy pudełka

psik: zatem wierzchołek nie należy do dziedziny a najmniejsza możliwa wartość będzie nieco mniejsza od 10, to jedyne wytłumaczenie.

Basiek: x−> 10

Saizou : zobaczymy w poniedziałek albo we wtorek bo tak liczę że będę miał już poprawiony sprawdzian

psik: x<10

Basiek: Nie napisałam, że x=10, tylko x dąży do 10−tki, której notabene nie może osiągnąć

psik: mm , to chyba coś z limens , ale ja się nie znam

Basiek: *limes Granica. x−> 10

psik: no też mówię że się nie znam

Saizou : to nie mój poziom

Bezimienny: Basiek widze probuje juz matematyke ze studiow x)

Basiek: W każdym razie, innego rozwiązania nie widzę. Bardzo możliwe, że nauczycielka się machnęła i wzięła zadanie optymalizacyjne z jakiejś starszej książki. Wiesz, czy komuś w klasie wyszło coś konstruktywnego?

Basiek: @Bezimienny− Basiek miała to w liceum, ale takie podstawowe sprawy

Saizou : mój kolego podzielił sobie tę kartkę na 6 kwadratów każdy o wymiarach 10x10 i zbudował pudełko z zamknięciem

Basiek: Takie pudełko się przecież nie złoży...?

Saizou : wiem a teraz czekam do następnego tygodnia z wynikami

Nienor: Narysuj funkcję w dziedzinie i zobacz jaka jest wartość najmniejsza. Z pochodnej ekstremum wychodzi w wierzchołku paraboli, co jest zresztą naturalne, wystarczy spojrzeć na wykres funkcji kwadratowej by wiedzieć, że wartość maksymalną lub minimalną ma w p wierzchołka paraboli. A ta cała funkcja wartości największej nie ma.

Nienor: Hmm... a tu wszystko ok z danymi jest?

Saizou : mój znajomy potwierdził treść zadania że jest OK

b.: tak jak stoi zadanie nie ma rozwiązania, chyba że dopuszczamy sytuację pudełka zdegenerowanego do pojedynczego odcinka strzelam, że chodziło o maksymalną objętość pudełka

Saizou : albo jest gdzieś błąd w zadaniu

krystek: Wymiary dna pudełka : (20−2*6,25)X(30−12,5)

Saizou : a można wiedzieć skąd to się wzięło?

Maslanek: A złożenie pudełka o podstawie odcinka to coś złego?

Saizou : @ Maslanek oczywiście że nie nawet jest to oryginalny sposób

Maslanek: P_podstawy=(20−2x)(30−2x) Z tego p = 12,5 oraz x∊(0,10). Więc Baśka ma rację, że: P_min = lim (x→10) (20−2x)(30−2x) = 0. Jak na moje

Saizou : to nie na moją głowę

Basiek: [Ja mam zawsze rację]

krystek: Nie licząc ,wziete dane z godz 16;09 a nie liczę . Nie ma rozwazania !

Maslanek: Idź się napij kawy

Maslanek: http://www.youtube.com/watch?v=0RIWmyfyhIo&feature=relmfu

Saizou : ale tam był błąd wymiar wyszły 12,5x12,5 cm co nie może być

Maslanek: Nie ma błędu x→10

Basiek: Maslanek− pierwszy porządny link od Ciebie. Wow. Btw. trzy na dziś wystarczą

Maslanek: Udław się tą kawą

Basiek: Teraz lubię Cię bardziej. ♥ http://www.youtube.com/watch?v=gjbLUxHNWdU&feature=related

Maslanek: Mnie czy oranżadę?

Maslanek: http://www.youtube.com/watch?v=Op8NEX_bCiM

Basiek: Ładne, dziękuję.

Saizou : wczoraj dostałem odpowiedź do tego zadania i wychodzi że nie istnieje taki x dla którego pole podstawy pudełka jest najmniejsze

Basia: bo nie istnieje; x∊(0;10) i minimum funkcji nie należy do tego przedziału

Saizou : no ale czy podstawa nie będzie najmniejsza jeśli x→10?